Abuse the symmetry of the first two constraints and multiply them together to get .
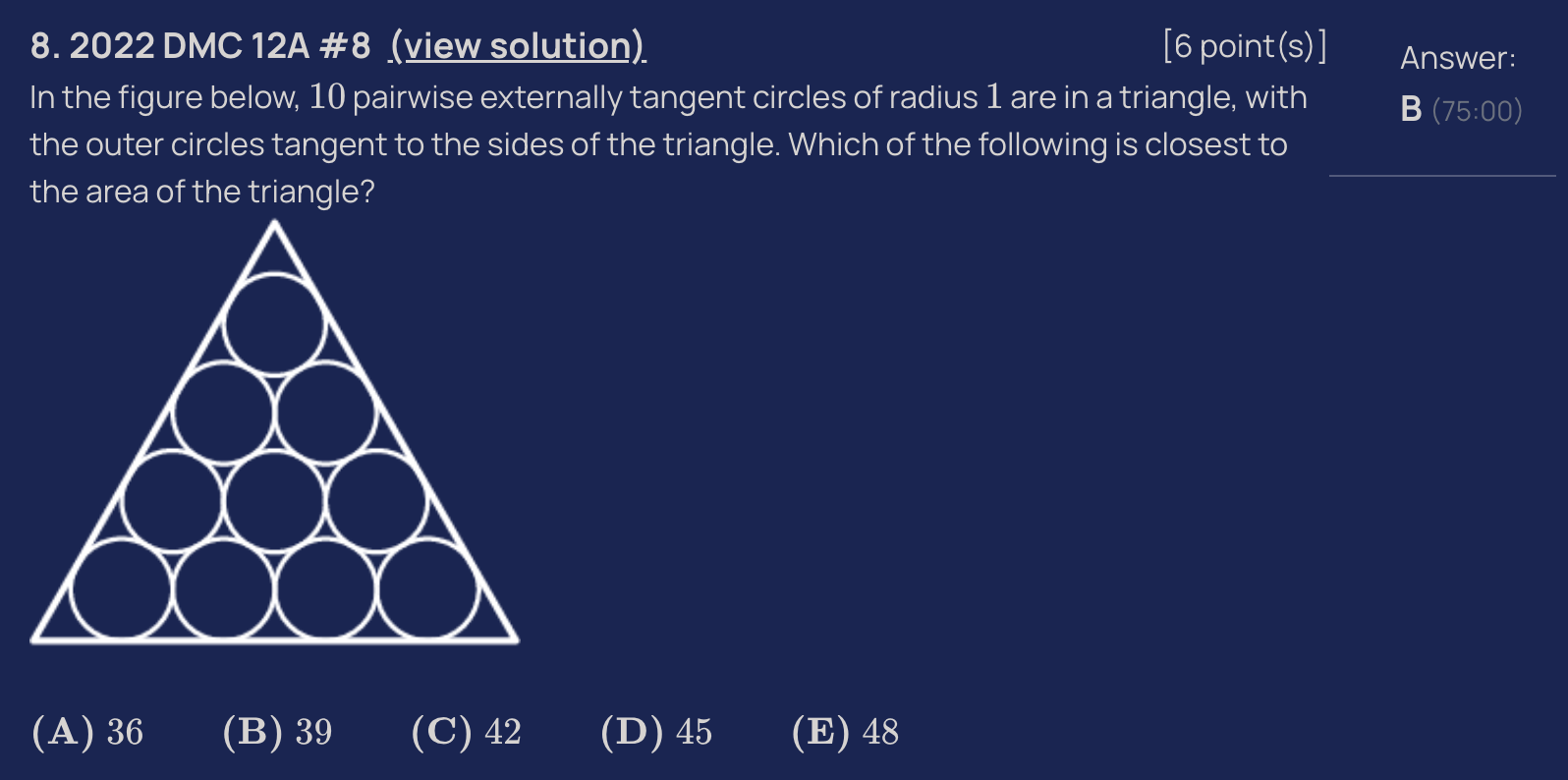The symmetric setup motivates finding the inradius of the large triangle, which is .
We can show that the condition is satisfied iff , where denotes the fractional part of . Using the fact that and also , we get that when increases by , decreases by a little more than . Since is small, this means our condition will hold for , or different values.
The possibilities for lie on the circle with diameter . Then, our ellipse constraint allows for at most possibilities of , and these possibilities will be symmetric in each quadrant. Therefore, the area-maximizing shape is a square inscribed in the circle.