Flow

Under construction, check back soon!

https://theory.stanford.edu/~trevisan/cs261/lecture15.pdf (MCMF LP duality)

• first, note that we can prove by duality that any fractional flow ⇐ any fractional cut
• so now it remains to show that the minimum fractional cut is precisely the minimum integer cut

interpret as edge-weights and find shortest path from to node as .

first, note that by min-cut assumption (and this is equivalent).

now, consider all possible cuts . we will show that there exists some value of T in such that .

consider . by linearity, the contribution of each edge to this expectation is precisely . therefore , which means there must exist some such that .

Karger’s randomized algorithm for min-cut: https://theory.stanford.edu/~trevisan/cs261/lecture13.pdf https://en.wikipedia.org/wiki/Karger%27s_algorithm

Konig’s Theorem

The theorem states that the maximum matching in any bipartite graph is equal to the minimum vertex cover. This follows directly from min-flow min-cut.

Dilworth’s Theorem

Statement

This theorem states that the minimum path cover in a transitive DAG has the same cardinality as the maximum antichain of that DAG. Here, an antichain refers to a set of nodes such that no node in the set is reachable from another node in the set. Intuitively, this captures how “wide” the DAG is (and indeed, this metric is also referred to as the width of a poset).

Note that this theorem does not hold for non-transitive DAGs. For instance, consider the following graph:

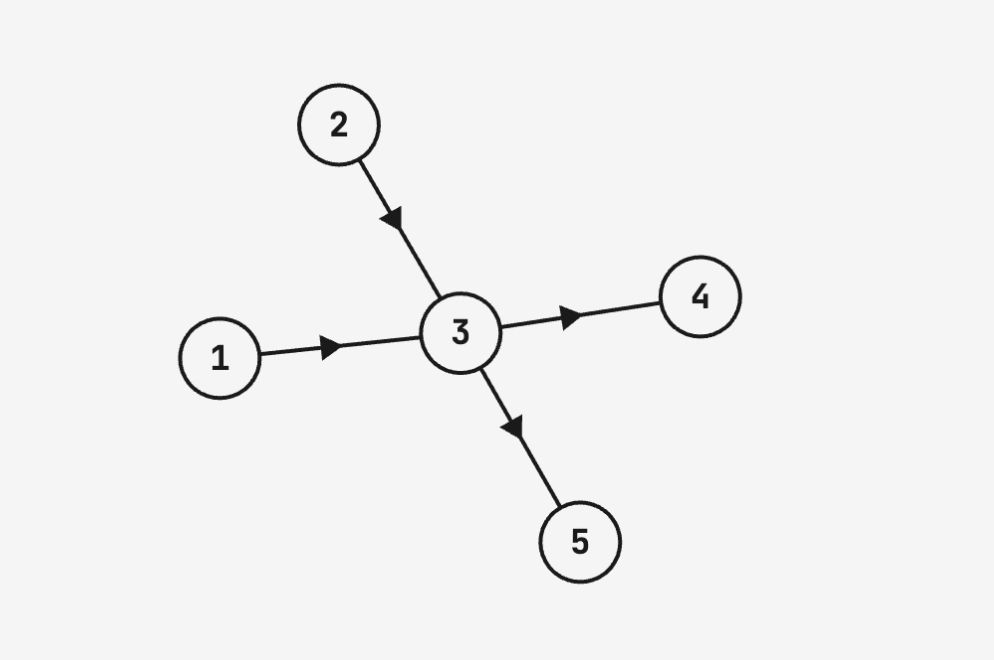
The maximal antichain has size 2 (for instance or ), but the minimal path cover has size . This gap is closed, however, when the transitive edges and are added.

Equivalently, we could just allow paths in the path cover to have overlapping vertices. Then, in the above graph we would be able to take paths and as a cover, which requires two chains as expected.

Proof (Inductive)

There are two proofs here, but in my opinion the first one is much nicer.

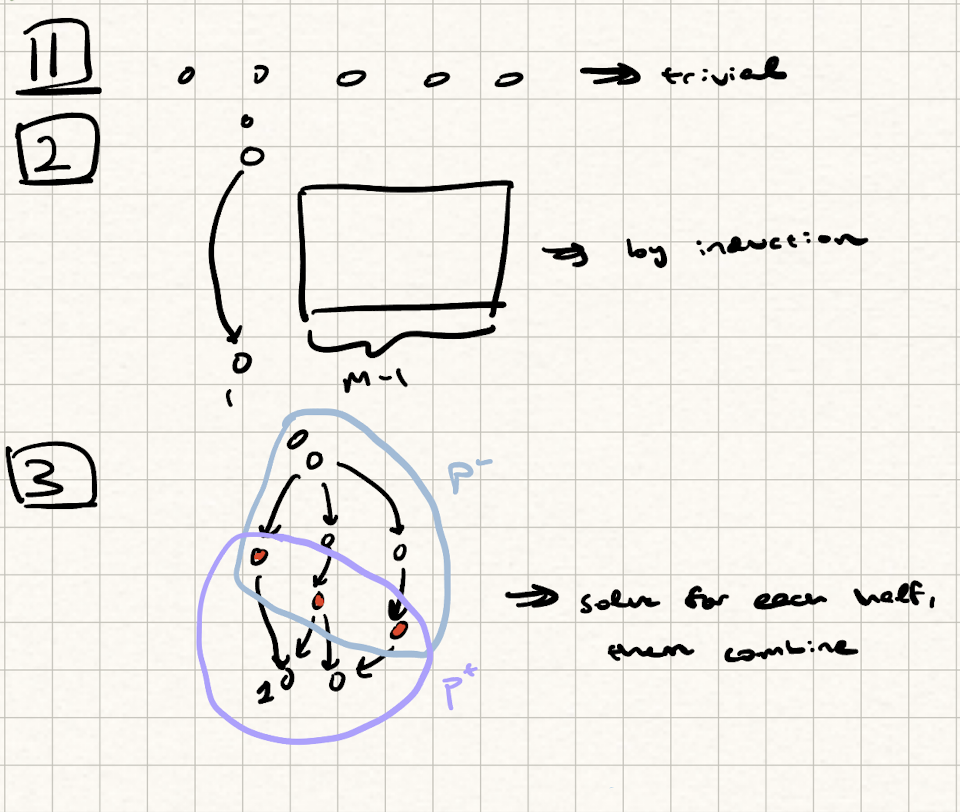
An illustration of the intuitive ideas behind the first proof. In Case 3, the red nodes denote an anti-chain.

Proof (Konig’s)

First of all, it’s clear that the minimum path cover requires a number of chains at least equal to the maximal antichain. Therefore, we just need to show there exists a path cover with exactly that amount.

We can transform the minimum path cover problem to one of bipartite matching like so:

1. For each node, split it into in and out.
2. If there exists an edge in the DAG, draw an undirected edge from to .
3. Now each matched edge corresponds to an edge in our path cover. Note that minimizing the number of different chains is equivalent to maximizing the total number of edges, therefore this is the same problem.

To finish, we can apply Konig’s theorem. Observe that if we have an antichain, the set of all nodes not in that antichain must form a vertex cover. Otherwise, there would exist an edge between two nodes in the antichain, which violates the definition.

Konig’s theorem then states that if we can match at most edges, we can also construct a vertex cover with nodes, which corresponds to an antichain with nodes. At the same time, a matching with edges corresponds to a path cover of chains, therefore we are done.