Statement
You are given a binary tree with weighted nodes. Operating on edge swaps and for cost . Find the minimum total cost to operate on every edge exactly once, in any order. (https://qoj.ac/problem/4054)
Solution
First, observe that the left and right subtrees of a node are almost independent. Any configuration in which edges from the two subtrees are interleaved can be shown to be equivalent to one of two cases:
- All edges in the left subtree are operated before any edge in the right subtree.
- All edges in the right subtree are operated before any edge in the left subtree.
Assume WLOG that we operate the left subtree first, and let our root node be . Then, for the left subtree, we only care about two things:
- which node node ends up in
- which node from the left subtree ends up in position
Then, we can plug into the right subtree and minimize. This yields a pretty simple solution, where dp[u][x][y] represents the minimum cost to delete all edges in the subtree of , while moving to and moving to .
An important observation from here is to notice that and must satisfy , otherwise it’s surely impossible. This immediately reduces the number of states to only . To optimize our runtime to also be , note that we can optimize dimensions incrementally, rather than all at once.
For instance, consider the case where our operation order is , then left subtree, then right subtree.
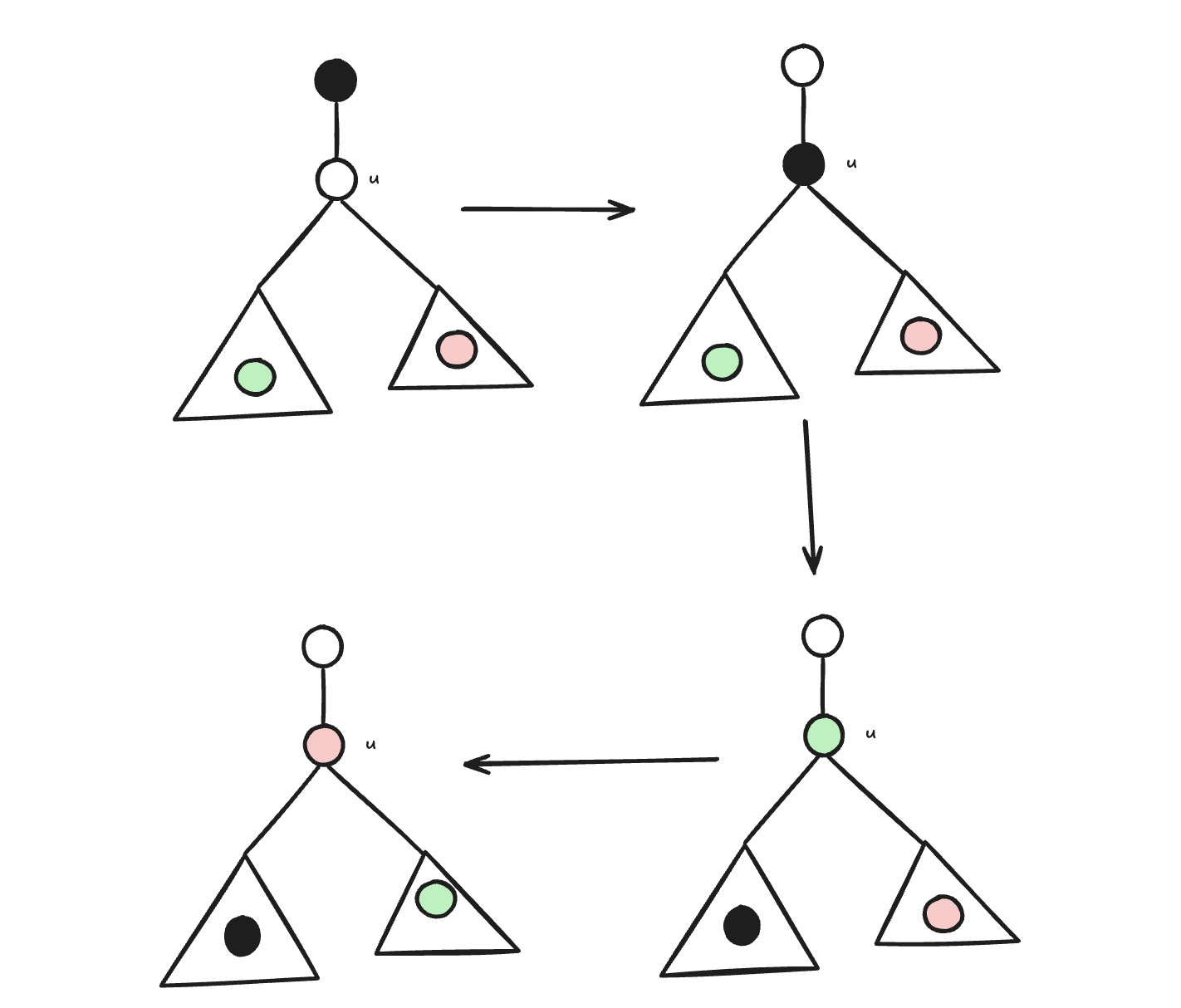
In the last step, since we care about neither where the green node ultimately settles nor what the red node is, we can precompute into_r[x] as the minimum cost to move (the green node) anywhere into the right subtree and get any node out. We can show that in total over all , this step takes only time. Similar pre-computation can be applied in other cases, leading to a overall runtime of .
My submission: https://qoj.ac/submission/1878265