Optimal Constructives

Optimal Constructives

10/20

---

Warm-Up

You are given an array of $2n$ integers. You want to put them into pairs $(x_1,y_1),(x_2,y_2)\dots (x_n,y_n)$ such that each integer is in exactly one pair. Your score is defined as the sum of $|y_i-x_i|$ over all pairs. What’s the maximum score you can achieve?

Example: $a=[1,3,2,4]\Rightarrow (1,3),(2,4)$

---

Optimal Constructives

Construct ___ such that ___ is maximized/minimized.

---

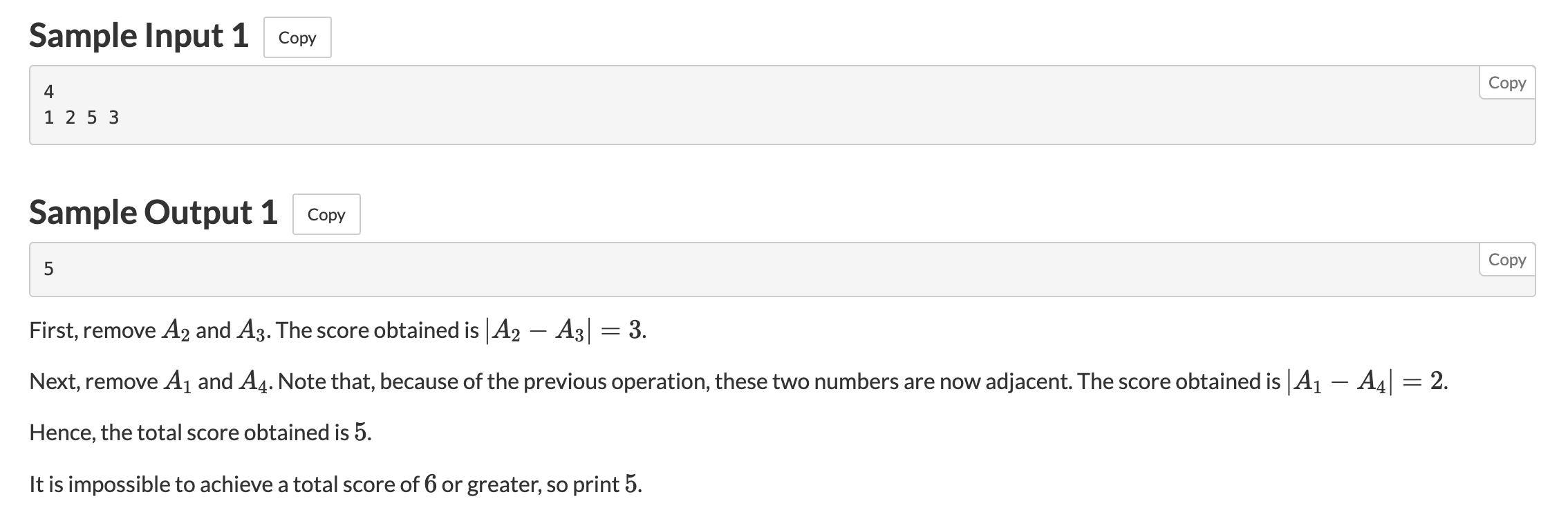
Adjacent Delete

---

Solution

(for now, assume $n$ is even) Ideally, we always pair the largest $\frac{n}{2}$ elements with the smallest $\frac{n}{2}$ elements. The cool thing is it turns out that this is always possible!

We can use a simple inductive proof. When $n=0$, it is obviously always possible. Then, when $n>0$, note that there must always be a “large” element adjacent to a “small” element. Therefore, we can simply delete this pair, and recurse to $n-2$.

$n$ odd case is left as an exercise to the reader/viewer.

---

Manhattan Pairs

---

Solution

The idea is similar to that of Adjacent Delete. Let’s shift our coordinate axes such that exactly half the points are above the $x$-axis, and exactly half the points are to the right of the $y$-axis. Then, our goal is to pair points in the first quadrant with points in the third quadrant, and points in the second quadrant with points in the fourth quadrant.

Again, it turns out that this is always possible!

---

Bounds

The next two problems involve finding good upper/lower bounds on the answer that will decrease our search space significantly.

---

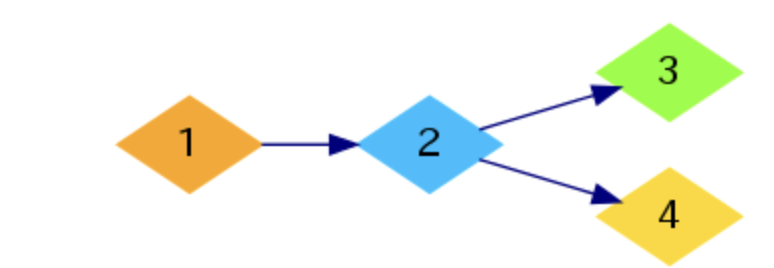
Mr Kitayuta’s Technology

---

Solution

First observe that we can solve each weakly connected component separately.

Now, notice that in a component of $n$ nodes, we can always satisfy all relations by using only $n$ edges, simply by connecting the entire component in a cycle. We also definitely can’t use less than $n-1$ edges, otherwise the component won’t be connected anymore. Therefore, the question becomes: can we satisfy all required relations in this component using only $n-1$ edges (sound familiar?)

---

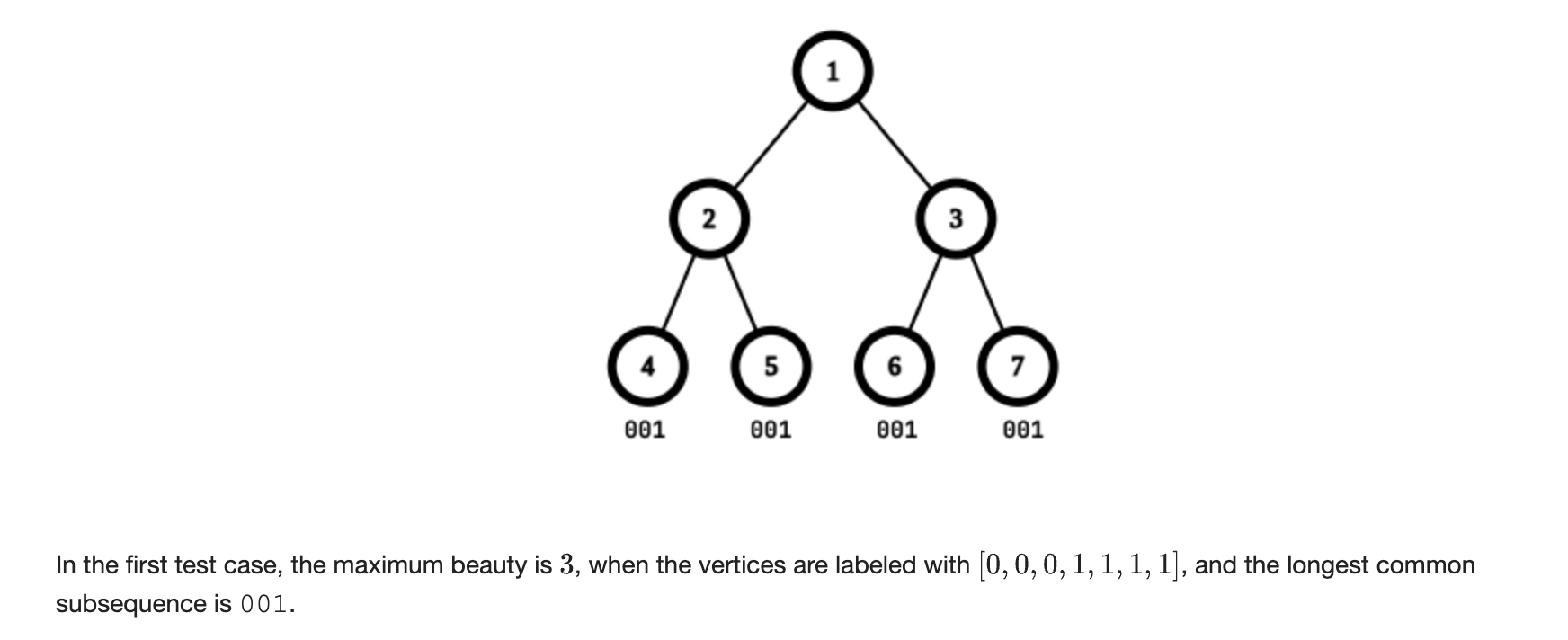
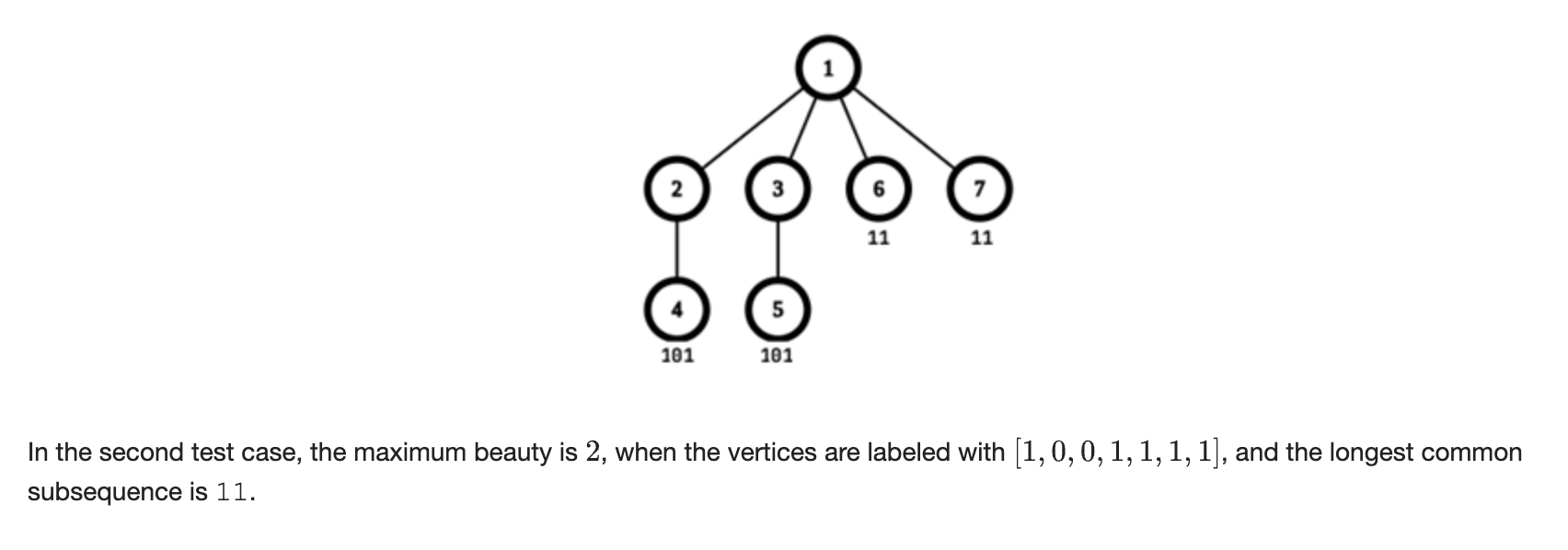
Maple and Tree Beauty

---

Solution

Let $d$ be the minimum depth of any node. Then, it turns out the answer is always at least $d-1$ (how?) Therefore, we just need to know whether we can achieve an answer of exactly $d$ or not, which can be done via a subset sum DP.