Statement
You are given a rooted tree with nodes and height . Assign integer to every node such that the value of the tree is maximized, where value is defined as
and denotes the nodes in the subtree of . (https://qoj.ac/contest/2669/problem/15459)
Solution
The simplest DP state is to let dp[u][m][f] denote the maximum value of subtree given that the MEX of this subtree is and there are “free” values that don’t contribute to any mex.
For instance, consider the above tree. The states of subtrees 2, 3, and 4 are , , and respectively. When we combine these three states along with the state of our root, the new resultant state is . Then, we can use the free values to increase the mex of our subtree, leading to a final state of .
Therefore, the most naive method of transitioning is essentially a convolution where . Then, we can use some of our free values to increase our mex: that is, transitions to .
Naively implementing this is very slow, but we can actually speed this DP up to by simply transitioning to both and . This corresponds to fixing one subtree to provide the maximum MEX and ignoring the MEX of the rest, which allows for our transitions to be optimized via pre-computation. For more details, see my implementation here.
It seems like the most difficult decision to make in our DP is picking which subtree to provide the maximum MEX. Let’s consider fixing our choices for every node first, then optimizing based on that. For each node, we will draw a red edge to the child subtree with the maximum MEX.
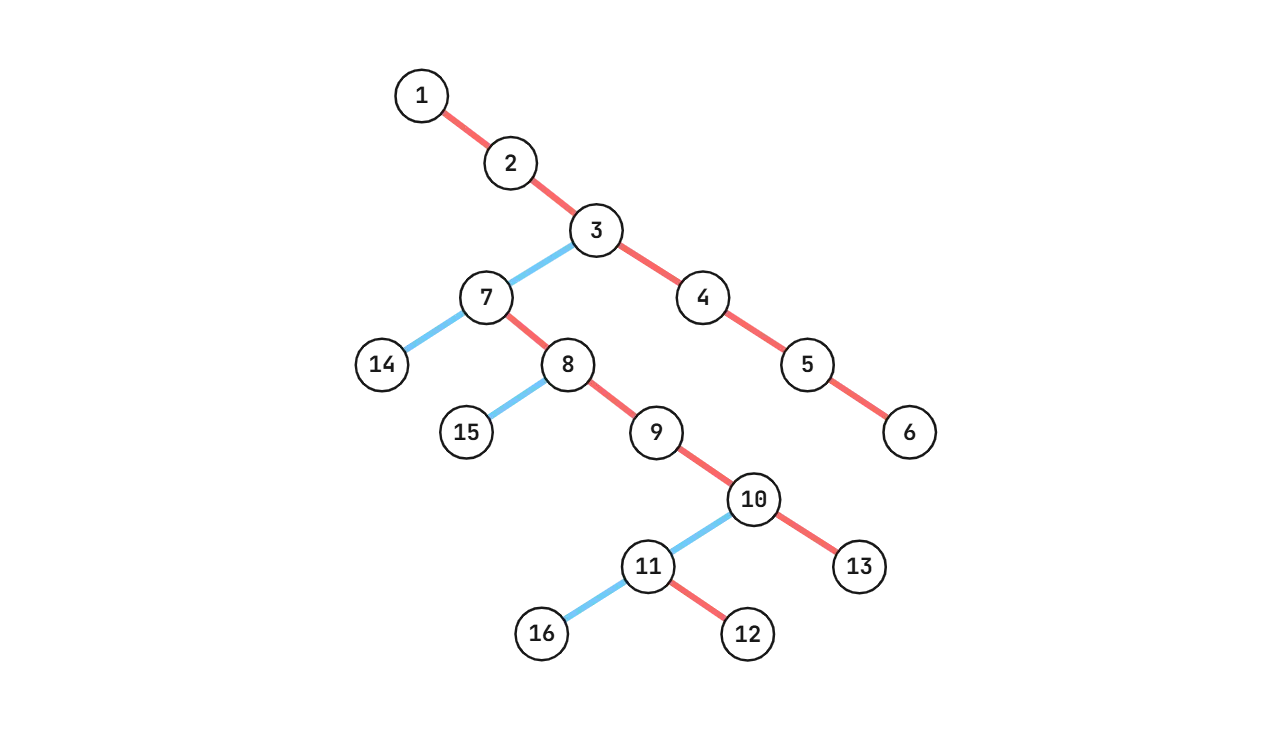
As described in our DP, if is the red child of , , where is the set of nodes consumed by to increase its MEX. For instance, in the first tree shown, , , and . If is in , we will refer to node as a stepping stone for node .
Since we’ve fixed the red edges, our job is now to decide the sets. To do this, we analyze the contribution of each individual node. Consider node 16. It can used as a stepping stone for any of its ancestors (including itself), so which one should we pick?
Note that if we choose to use node 16 as a stepping stone for node 10, it will not only increment , but also , , and , since they connect to node 10 via red edges. Therefore, if 16 is placed in , it will have a contribution of . In comparison, placing it in only contributes , and placing it in or only contributes .
We can thus define a new DP state: dp[u][mx][len] denotes the maximum possible value of subtree given that node can contribute a maximum of and is at the end of a red chain with nodes. For instance, node in the above diagram would be in the state dp[8][3][2]. The 3 represents that node can have contribution by becoming a stepping stone for node , and the represents the current length of node ‘s chain (consisting of nodes and ). Transitions are left as an exercise to the reader.
A good thing about reformulating our DP in this way is that it admits an important greedy observation. Let be a blue child (e.g. node 7 or 15 in above diagram), and mx be its maximum possible contribution (same as our DP above). Then, one of the following two conditions must be true:
- All red chains in the subtree of have no more than
mxnodes. - The red chain rooted at has more than
mxnodes.
To prove this, consider the case where the red chain rooted at has fewer than mx nodes, but one of its children starts a chain with more than mx nodes. Then, it’s never less optimal to simply connect this child to node instead.
TO BE CONTINUED
My submission: https://qoj.ac/submission/1881469